当前：首页 > 高考网 > 科目辅导 > 数学

高中数学最好的办法就是整理思维导图

高中数学最好的办法就是整理思维导图

高三数学期末考知识点，统计知识点集锦。备战高三期末考，时间紧任务重，如何快速的理清复习思路呢，最好的办法就是整理高中数学的思维导图，根据思维导图上知识点的联系性进行有计划的复习，这样才更有效率。

1：简单随机抽样

(1)总体和样本

①在统计学中 ， 把研究对象的全体叫做总体.②把每个研究对象叫做个体.③把总体中个体的总数叫做总体容量.

④为了研究总体 的有关性质，一般从总体中随机抽取一部分： x1，x2 ， ....，xx 研究，我们称它为样本.其中个体的个数称为样本容量.

(2)简单随机抽样，也叫纯随机抽样。就是从总体中不加任何分组、划类、排队等，完全随

机地抽取调查单位。特点是：每个样本单位被抽中的可能性相同(概率相等)，样本的每个单位完全独立，彼此间无一定的关联性和排斥性。简单随机抽样是其它各种抽样形式的基础。通常只是在总体单位之间差异程度较小和数目较少时，才采用这种方法。

(3)简单随机抽样常用的方法：

①抽签法②随机数表法③计算机模拟法③使用统计软件直接抽取。

在简单随机抽样的样本容量设计中，主要考虑：①总体变异情况；②允许误差范围；③概率保证程度。

(4)抽签法：

①给调查对象群体中的每一个对象编号；②准备抽签的工具，实施抽签；

③对样本中的每一个个体进行测量或调查

(5)随机数表法：

2：系统抽样

(1)系统抽样(等距抽样或机械抽样)：

把总体的单位进行排序，再计算出抽样距离，然后按照这一固定的抽样距离抽取样本。第一个样本采用简单随机抽样的办法抽取。 K(抽样距离)=N(总体规模)/n(样本规模)

前提条件：总体中个体的排列对于研究的变量来说，应是随机的，即不存在某种与研究变量相关的规则分布。可以在调查允许的条件下，从不同的样本开始抽样，对比几次样本的特点。如果有明显差别，说明样本在总体中的分布承某种循环性规律，且这种循环和抽样距离重合。

(2)系统抽样，即等距抽样是实际中最为常用的抽样方法之一。因为它对抽样框的要求较低，实施也比较简单。更为重要的是，如果有某种与调查指标相关的辅助变量可供使用，总体单元按辅助变量的大小顺序排队的话，使用系统抽样可以大大提高估计精度。

3：分层抽样

(1)分层抽样(类型抽样)：

先将总体中的所有单位按照某种特征或标志(性别、年龄等)划分成若干类型或层次，然后再在各个类型或层次中采用简单随机抽样或系用抽样的办法抽取一个子样本，最后，将这些子样本合起来构成总体的样本。

两种方法：

①先以分层变量将总体划分为若干层，再按照各层在总体中的比例从各层中抽取。

②先以分层变量将总体划分为若干层，再将各层中的元素按分层的顺序整齐排列，最后用系统抽样的方法抽取样本。

(2)分层抽样是把异质性较强的总体分成一个个同质性较强的子总体，再抽取不同的子总体中的样本分别代表该子总体，所有的样本进而代表总体。

分层标准：

①以调查所要分析和研究的主要变量或相关的变量作为分层的标准。

②以保证各层内部同质性强、各层之间异质性强、突出总体内在结构的变量作为分层变量。

③以那些有明显分层区分的变量作为分层变量。

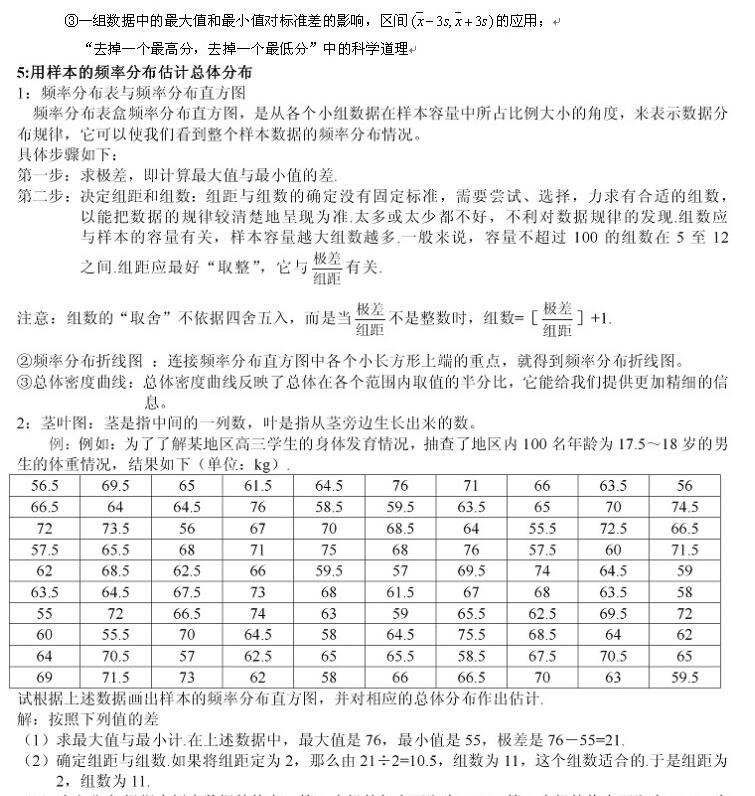
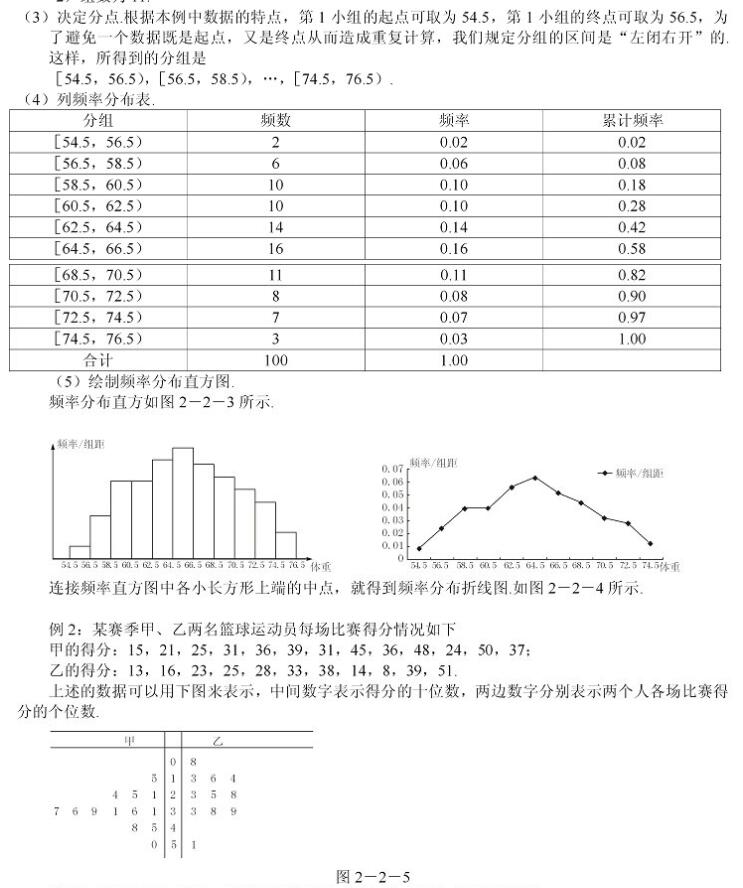
抽签法简介：

抽签法是先将调查总体的每个单位编号，然后采用随机的方法任意抽取号码，直到抽足样本的一种方法。应用于总体容量比较大的事务。由于简单易实施，应用非常广泛。
抽签法又称“抓阄法”。它是先将调查总体的每个单位编号，然后采用随机的方法任意抽取号码，直到抽足样本。一般地，抽签法就是把总体中的N个个体编号，把号码写在号签上，将号签放在一个容器中，搅拌均匀后，每次从中抽取一个号签，连续抽取n次，就得到一个容量为n的样本。
有时需用这样一个骰子，这个骰子上0-9的数字的出现，都应该有同等的概率，因而一个立体正20方形的骰子，才可以满足上述需要。例如：要从1000个样本中中选出10个样本，则把这个骰子转动3次，以最先得得的数字为百位，第2次为十位，第3次得到为个位，组成一个数，反复转动骰子，可得到一组数据，即为样本的序号。